Newton in 1672 noted how a ball’s flight was affected by spin. In 1742, Robins showed that a transverse aerodynamic force could be detected on a rotating sphere. Earlier theories also gave a simple analysis for a “frictionless fluid,” which showed that the side force was proportional to the free stream velocity and the rotational speed. In 1853, the first explanation of the lateral deflection of a spinning ball or cylinder is credited to German physicist Heinrich Magnus from which the phenomenon derives it
name, the “Magnus Effect”. This, all presented well before the introduction of the boundary-layer concept by Prandtl in 1904.
The commonly accepted explanation is that a spinning object creates a whirlpool of rotating fluid about itself. On the side where the motion of the whirlpool is in the same direction as that of the direction of flow to which the object is exposed, the velocity will be increased. On the opposite side, where the directions are opposed, the velocity will be decreased. Then, according to Bernoulli’s principle, the pressure is lower on the side where the velocity is greater, and consequently there is an unbalanced force at right angles to the fluid flow. This is the Magnus effect.
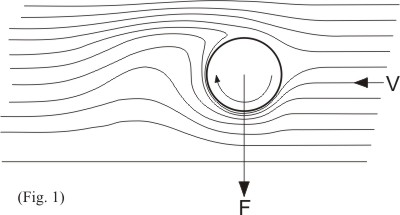
Studies agree that the Magnus force results from the asymmetric distortion of the boundary layer displacement thickness caused by the combined spinning and flow past the sphere. The motion imparted by the spinning cylinder to the boundary layer affects the manner in which the flow separates from the surface at the rear. Boundary layer separation is delayed on the side of the spinning object that is moving in the same direction as the free stream flow, while the separation or shear occurs prematurely on the side moving against the free stream flow creating turbulence in the down stream wake. The resulting turbulent wake then shifts toward the side moving against the free stream flow. As a result, flow past the object is deflected, and the resulting change in momentum flux causes a force in the opposite direction (see figure 1).
This phenomenon is influenced by the conditions within the layer next to the body, known as the boundary layer. Certain results of the force of the spinning body introduce anomalies within the layer, such as creating turbulent flow on one side and not the other.
The following equation demonstrates the manipulation of characteristics needed to determine the lift force generated by inducing a mechanical rotation on a cylinder:
F = 1/2 . ρ . V2. A . Cl
F = lift force
V = velocity of flow
A = cross-sectional area of cylinder
Cl = lift coefficient
ρ = density of the fluid
The lift coefficient is the ratio between the weight of the cylinder and the fluid density, the velocity squared, and the cross-sectional area of the cylinder. Lift coefficient is dependent on:
The Lift coefficient may be determined from graphs of experimental data using Reynolds number and spin ratio. Typical lift coefficients of a cylinder with smooth surface range from 0.2 to 0.6 with spin ratios ranging from 0.5 to 4.5.